Cross-Validation: The Gold Standard for Model Evaluation

When we build a machine learning model, our primary goal is for it to generalize well to new, unseen data. A common way to estimate this is to split our data into a training set and a testing set. We train the model on the training set and evaluate it on the testing set.

But this approach has a weakness. What if we were just unlucky (or lucky) with our split? What if the testing set happened to contain a lot of easy-to-predict data points, making our model seem better than it is? Or what if it contained a lot of unusual outliers, making it seem worse?

The performance score from a single train/test split can be highly variable. To get a more reliable estimate of our model’s performance, we can use a technique called cross-validation.

K-Fold Cross-Validation

The most common type of cross-validation is K-Fold Cross-Validation. It works as follows:

1. Split: Randomly split the entire dataset into ‘K’ equal-sized subsets, or “folds.”
2. Iterate: For each fold, from 1 to K: a. Hold out the current fold and use it as the validation set. b. Use all the other K-1 folds as the training set. c. Train a new model on the training set and evaluate it on the validation set. d. Keep the evaluation score and discard the model.
3. Average: After K iterations, you will have K different performance scores. The final performance of your model is the average of these K scores.

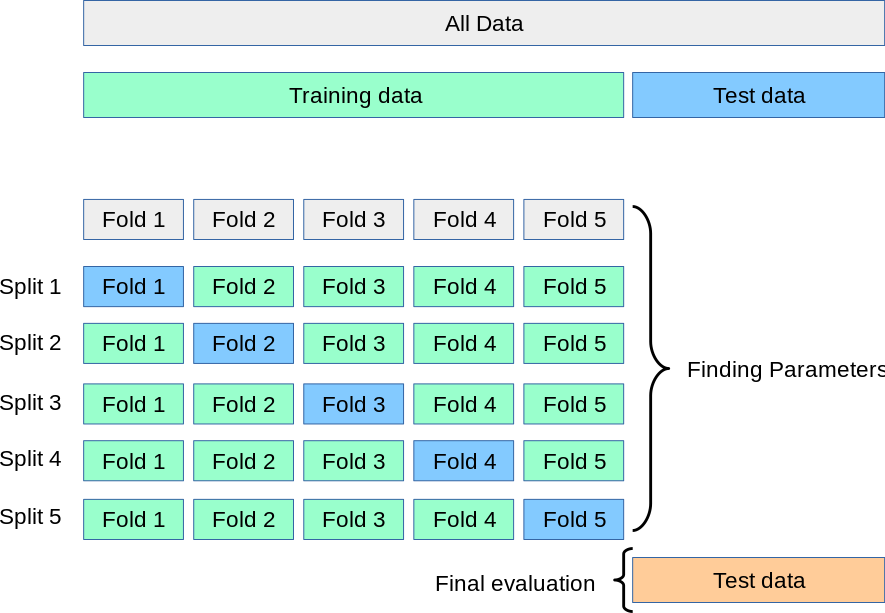Image from the Scikit-Learn documentation.

A common value for K is 5 or 10. This process gives a much more robust estimate of the model’s performance on unseen data because it uses every data point for both training and validation over the course of the K iterations.

When to Use Cross-Validation

• Model Selection: If you are comparing different algorithms (e.g., Logistic Regression vs. Random Forest), cross-validation can give you a better estimate of which one will perform better in the real world.
• Hyperparameter Tuning: As we’ve seen previously, cross-validation is a core component of GridSearchCV and RandomizedSearchCV, ensuring that we select hyperparameters that generalize well.
• Reliable Performance Estimate: When you need a trustworthy measure of your final model’s accuracy before deploying it.

The main drawback is that it’s more computationally expensive, as you need to train K models instead of just one.

Cross-Validation in Scikit-Learn

scikit-learn provides a simple way to perform cross-validation with the cross_val_score function.

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
import numpy as np

# --- 1. Generate Data ---
X, y = make_classification(n_samples=1000, n_features=20,
                           n_informative=10, n_redundant=0,
                           random_state=42)

# --- 2. Compare a single Train/Test split vs. Cross-Validation ---

# --- Single Split Evaluation ---
print("--- Single Train/Test Split ---")
# Create one specific split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
model = LogisticRegression(solver='liblinear')
model.fit(X_train, y_train)
score = model.score(X_test, y_test)
print(f"Accuracy on one specific test set: {score:.4f}")

# --- Cross-Validation Evaluation ---
print("\\n--- K-Fold Cross-Validation ---")
# Use the same model type
model_cv = LogisticRegression(solver='liblinear')

# Perform 10-fold cross-validation (cv=10)
# The function handles all the splitting, training, and scoring
scores = cross_val_score(model_cv, X, y, cv=10, scoring='accuracy')

print(f"Scores for each of the 10 folds: \\n{np.round(scores, 4)}")
print(f"\\nMean CV Accuracy: {scores.mean():.4f}")
print(f"Standard Deviation of CV Accuracy: {scores.std():.4f}")

# The result is a more reliable estimate of the model's true performance.
# The standard deviation gives us an idea of how much the performance varies across different data subsets.
# A model with a mean accuracy of 0.85 +/- 0.05 is more reliable than one with 0.85 +/- 0.2.

What the Code Does

1. Single Split: We perform a standard 70/30 train/test split and calculate the accuracy of a LogisticRegression model. The result is a single number.
2. Cross-Validation: We use cross_val_score to perform 10-fold cross-validation on the entire dataset.
   • estimator=model_cv: The model object to use.
   • X, y: The data and labels.
   • cv=10: The number of folds (K).
   • scoring='accuracy': The metric to use for evaluation.
3. Results: The function returns an array of 10 scores, one for each fold. We can then calculate the mean and standard deviation of these scores. The mean gives us our robust performance estimate, and the standard deviation tells us how stable that estimate is.

Conclusion

While a simple train/test split is a good first step, K-Fold Cross-Validation is the industry standard for getting a reliable estimate of a model’s generalization performance. It’s an essential technique for robustly comparing models and for tuning hyperparameters, ensuring that you build models that are not just accurate on your current data, but on future data as well.